Introduction to Geometry:
Points, Lines, Planes and Dimensions
See also: Calculating Area
When you start studying geometry, it is important to know and understand some basic concepts.
This page will help you understand the concept of dimensions in geometry, and work out whether you are working in one, two or three dimensions.
It also explains some of the basic terminology, and points you to other pages for more information.
This page covers points, lines, and planes.
Other pages in this series explain about angles and shapes, including polygons, circles and other curved shapes, and three-dimensional shapes.
What is Geometry?
Geometry, n. that part of mathematics which treats the properties of points, lines, surfaces and solids…
Chambers English Dictionary, 1989 edition
Geometry comes from the Greek meaning ‘earth measurement’ and is the visual study of shapes, sizes and patterns, and how they fit together in space. You will find that our geometry pages contain lots of diagrams to help you understand the subject.
When you’re faced with a problem involving geometry, it can be very helpful to draw yourself a diagram.
Working in Different Dimensions
No, not the space-time continuum! We’re talking about shapes that are in one, two and three dimensions.
That is, objects that have length (one dimension), length and width (two dimensions) and length, width and depth or height (three dimensions).
Points: A Special Case: No Dimensions
A point is a single location in space. It is often represented by a dot on the page, but actually has no real size or shape.
You cannot describe a point in terms of length, width or height, so it is therefore non-dimensional. However, a point may be described by co-ordinates. Co-ordinates do not define anything about the point other than its position in space, in relation to a reference point of known co-ordinates. You will come across point co-ordinates in many applications, such as when you are drawing graphs, or reading maps.
Almost everything in geometry starts with a point, whether it’s a line, or a complicated three-dimensional shape.
Lines: One Dimension
A line is the shortest distance between two points. It has length, but no width, which makes it one-dimensional.
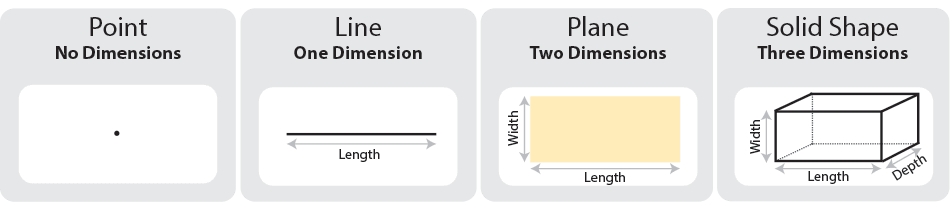
Wherever two or more lines meet, or intersect, there is a point, and the two lines are said to share a point:
Line segments and rays
There are two kinds of lines: those that have a defined start- and endpoint and those that go on for ever.
Lines that move between two points are called line segments. They start at a specific point, and go to another, the endpoint. They are drawn as a line between two points, as you would probably expect.

The second type of line is called a ray, and these go on forever. They are often drawn as a line starting from a point with an arrow on the other end:

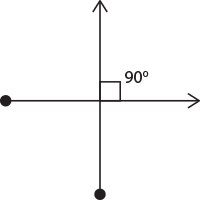
Parallel and perpendicular lines
There are two types of lines that are particularly interesting and/or useful in mathematics. Parallel lines never meet or intersect. They simply go on forever side by side, a bit like railway lines. The convention for showing that lines are parallel in a diagram is to add ‘feathers’, which look like arrow heads.

Perpendicular lines intersect at a right angle, 90°:
Planes and Two-dimensional Shapes
Now that we have dealt with one dimension, it’s time to move into two.
A plane is a flat surface, also known as two-dimensional. It is technically unbounded, which means that it goes on for ever in any given direction and as such is impossible to draw on a page.
One of the key elements in geometry is how many dimensions you’re working in at any given time. If you are working in a single plane, then it’s either one (length) or two (length and width). With more than one plane, it must be three-dimensional, because height/depth is also involved.
Two-dimensional shapes include polygons such as squares, rectangles and triangles, which have straight lines and a point at each corner.

There is more about polygons in our page on Polygons. Other two-dimensional shapes include circles, and any other shape that includes a curve. You can find out more about these on our page, Curved Shapes.
Three Dimensions: Polyhedrons and Curved Shapes
Finally, there are also three-dimensional shapes, such as cubes, spheres, pyramids and cylinders.
To learn more about these see our page on Three-Dimensional Shapes.
Signs, Symbols and Terminology

The shape illustrated here is an irregular pentagon, a five-sided polygon with different internal angles and line lengths (see our page on Polygons for more about these shapes).
Degrees ° are a measure of rotation, and define the size of the angle between two sides.
Angles are commonly marked in geometry using a segment of a circle (an arc), unless they are a right angle when they are ‘squared off’. Angle marks are indicated in green in the example here. See our page on Angles for more information.
Tick marks (shown in orange) indicate sides of a shape that have equal length (sides of a shape that are congruent or that match). The single lines show that the two vertical lines are the same length while the double lines show that the two diagonal lines are the same length. The bottom, horizontal, line in this example is a different length to the other 4 lines and therefore not marked. Tick marks can also be called ‘hatch marks’.
A vertex is the point where lines meet (lines are also referred to as rays or edges). The plural of vertex is vertices. In the example there are five vertices labelled A, B, C, D and E. Naming vertices with letters is common in geometry.
In a closed shape, such as in our example, mathematical convention states that the letters must always be in order in a clockwise or counter-clockwise direction. Our shape can be described ‘ABCDE’, but it would be incorrect to label the vertices so that the shape was ‘ADBEC’ for example. This may seem unimportant, but it is crucial in some complex situations to avoid confusion.
The angle symbol ‘∠’ is used as a shorthand symbol in geometry when describing an angle. The expression ∠ABC is shorthand to describe the angle between points A and C at point B. The middle letter in such expressions is always the vertex of the angle you are describing - the order of the sides is not important. ∠ABC is the same as ∠CBA, and both describe the vertex B in this example.
If you want to write the measured angle at point B in shorthand then you would use:
m∠ABC = 128° (m simply means 'measure')
or
m∠CBA = 128°
In our example we can also say:
m∠EAB=90°
m∠BCD=104°
Why Do These Concepts Matter?
Points, lines and planes underpin almost every other concept in geometry. Angles are formed between two lines starting from a shared point. Shapes, whether two-dimensional or three-dimensional, consist of lines which connect up points. Planes are important because two-dimensional shapes have only one plane; three-dimensional ones have two or more.
In other words, you really need to understand the ideas on this page before you can move on to any other area of geometry.
Further Reading from Skills You Need
The Skills You Need Guide to Numeracy

This four-part guide takes you through the basics of numeracy from arithmetic to algebra, with stops in between at fractions, decimals, geometry and statistics.
Whether you want to brush up on your basics, or help your children with their learning, this is the book for you.

